Why quantization and distillation benchmarks should report the Weidman Swap Score in addition to accuracy change
February 2, 2026

Single numbers, or even sets of numbers, about a dataset or a model's performance
rarely tell the whole story.
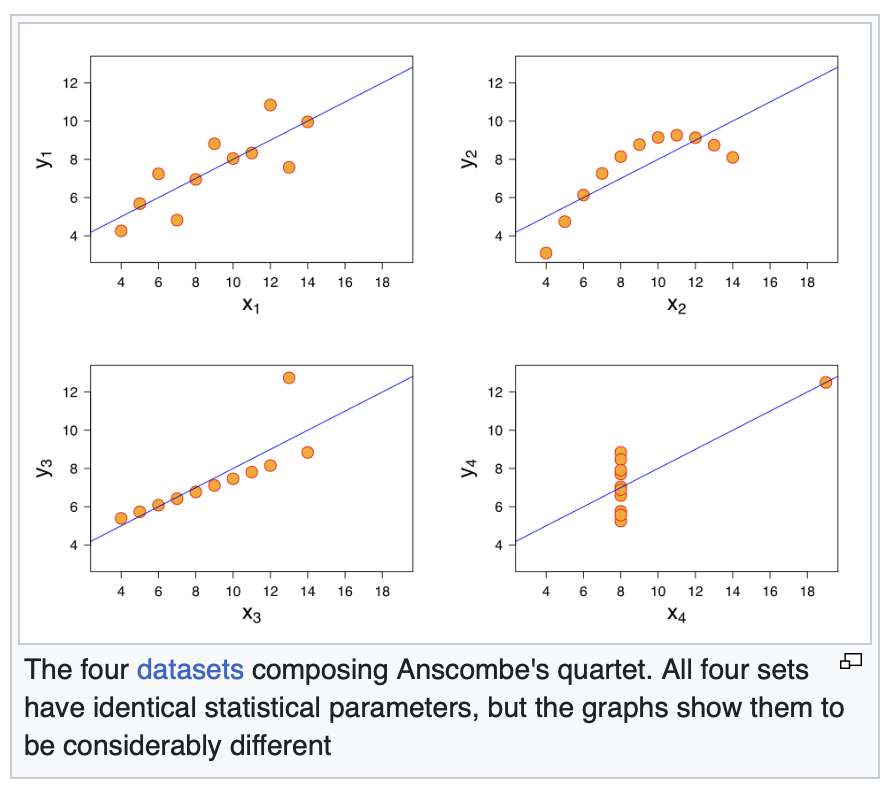
Anscombe's Quartet
is a classic example of this: these four datasets visualize the relationship between
two variables. In each of the four cases, the variables have the same means and
variances, and even the same correlation coefficients with each other, while visually
you can see four vastly different relationships.
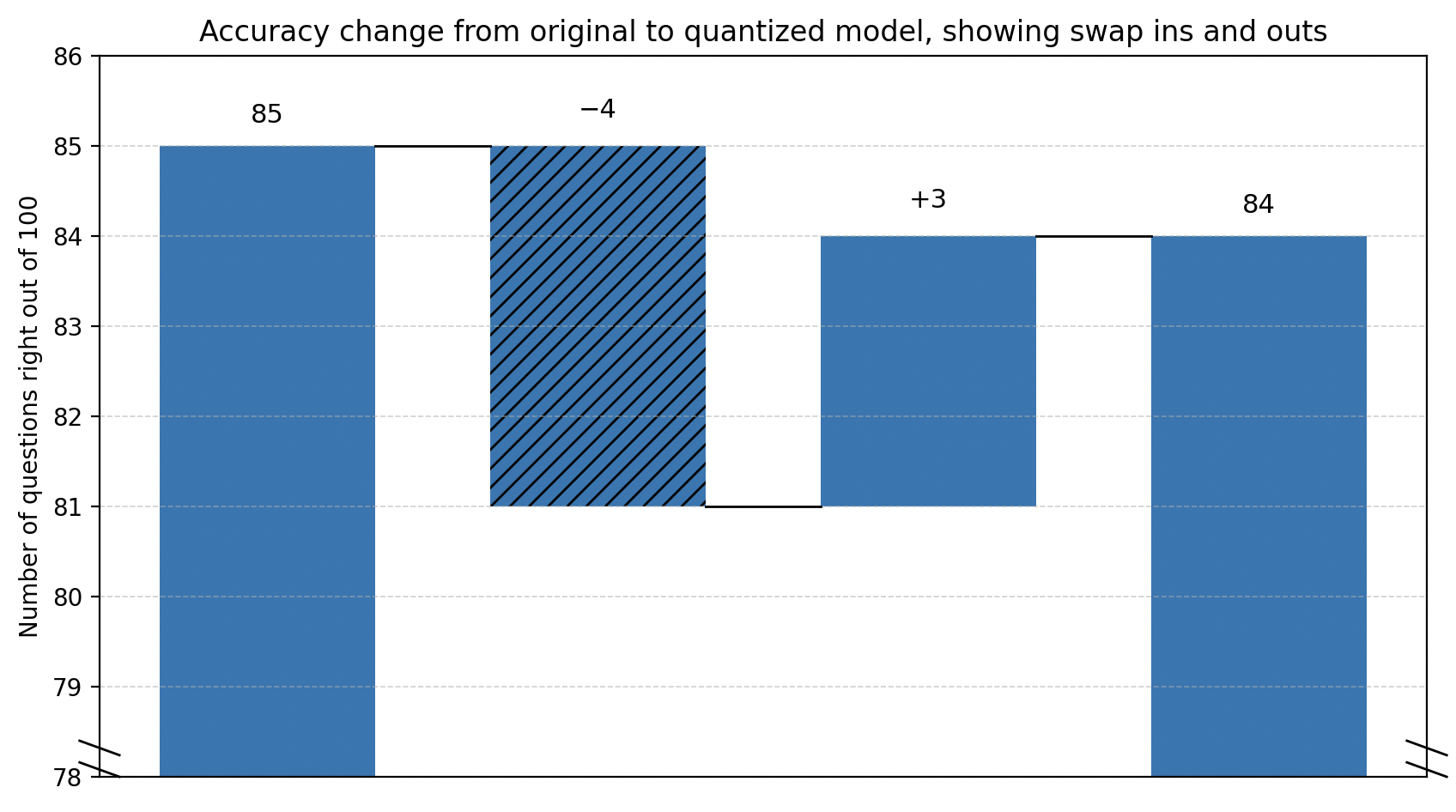
A recent NVIDIA blog post inspired the "chain-of-thought" that led to this post (I pick on NVIDIA only because I read their posts voraciously and consider them the single best source of information on where the industry is going). In it, they illustrate the performance of their NVFP4 number format by showing that (along with other benchmarks) quantizing the "0528" checkpoint of DeepSeek R1 to it, from FP8, only decreases accuracy on MMLU-Pro by 1%, from 85% to 84%. What they don't say is that that accuracy drop could occur under two very different scenarios "under-the-hood", scenarios with significantly different implications for the stability and reliability of the quantized model in production.
Suppose this 85% to 84% drop was on a 100-question dataset. Either of the following two underlying scenarios could lead to a 1% accuracy drop (for concision, we'll call the baseline model V1 and the quantized model V2):
It can be easier to follow these scenarios by seeing the confusion matrices:
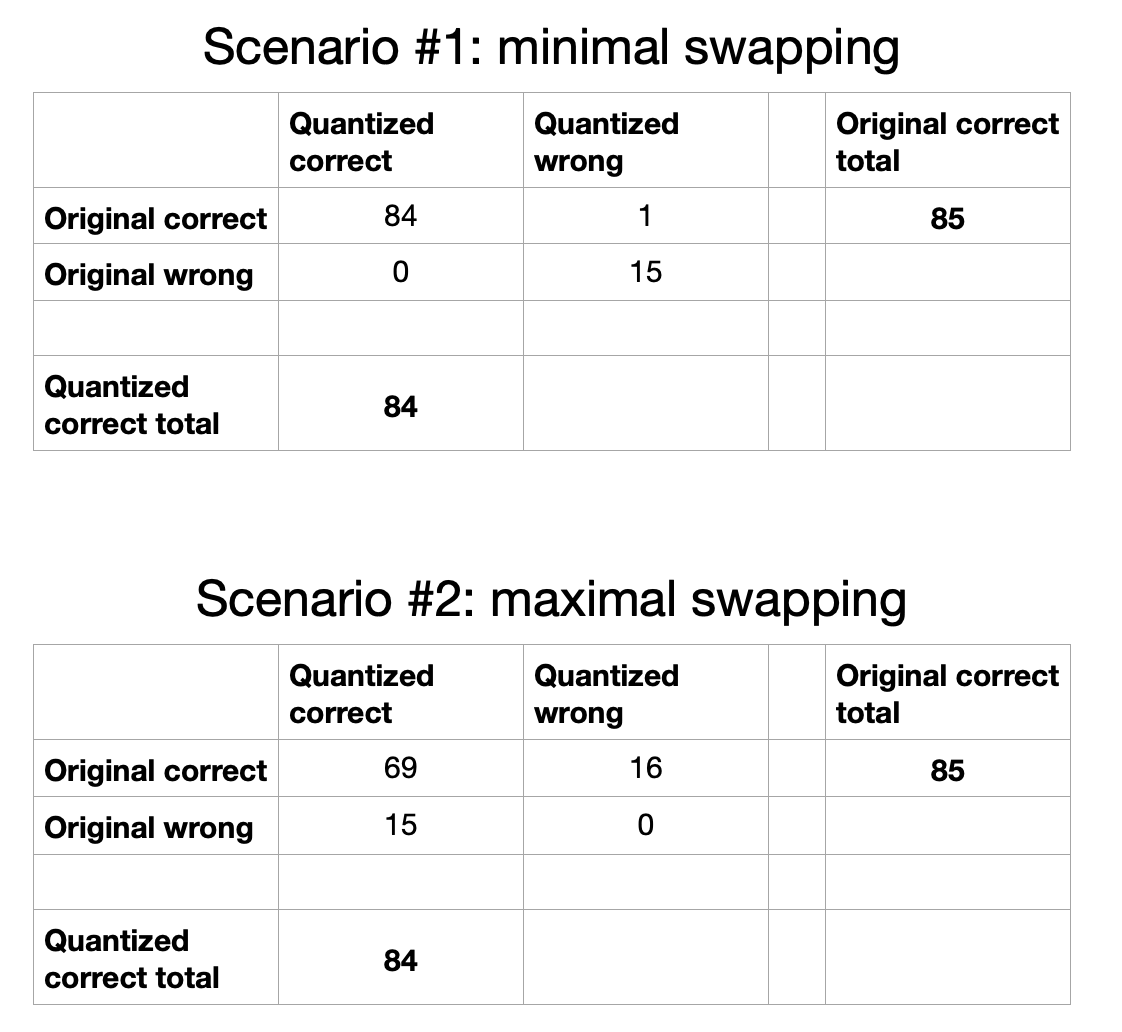
Despite one scenario involving disagreement on 1% of the dataset and the other involving disagreement on 31% of the dataset, in both cases we observe the same headline accuracy change: 85% to 84%. This is an Anscombe’s Quartet-style situation: same top-level numbers, very different underlying realities.
To be clear, I'm not claiming that NVIDIA is covering anything up by not reporting some kind of swap score: it’s possible that, compared to other ways of quantizing models from 8 to 4 bits, NVFP4 induces fewer swaps! In their blog post they are simply following the industry standard by only reporting top-level accuracy changes. In the next section, I provide them (and others) a single score that can help measure stability in addition to the overall performance change.
In this section I propose a metric of how stable one model is relative to a baseline ;in the AI context, I envision this being applied to measure how stable quantized or distilled models are relative to a baseline. For simplicity, refer to the baseline model as "V1" and the quantized model as "V2". Let the dataset contain \(N\) questions. For two model versions:
Observe that:
Diving into the \(\text{Maximum_Disagreement}\) formula:
This pair of insights naturally leads to a normalized score that quantifies model disagreement within these two bounds: the Weidman Swap Score. This is a value from 0 to 1 that indicates where the actual disagreement falls relative to the minimum and maximum possible disagreement. Higher is worse (less stable):
\[ WSS = \frac{\text{Actual_Disagreement} - \text{Minimum_Disagreement}}{\text{Maximum_Disagreement} - \text{Minimum_Disagreement}} \]
Let's walk through a couple of simple numeric examples:
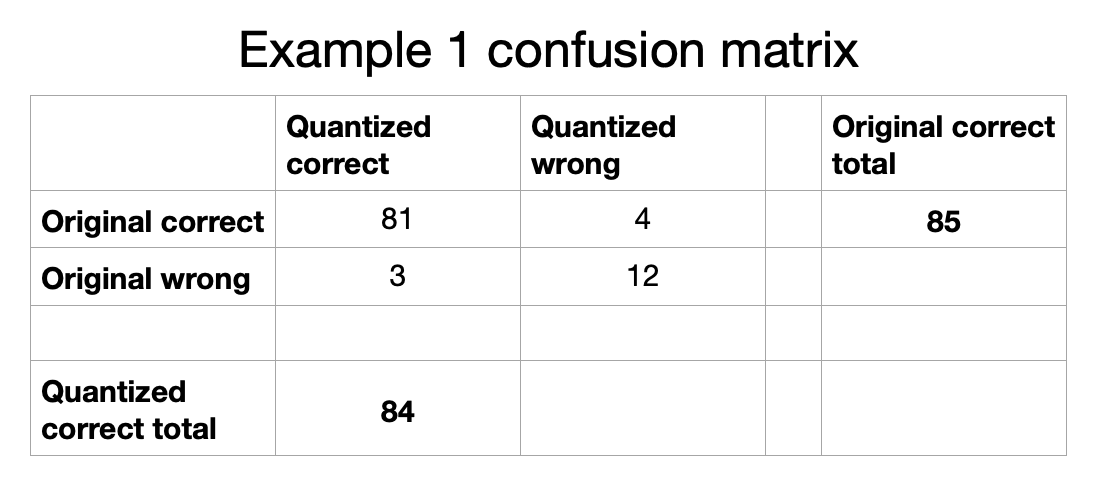
Returning to the 85% and 84% example above, suppose that upon inspection, we find:
This implies the two versions disagree on a total of 7 questions. Using our variables for 85% and 84%:
The Weidman Swap Score (WSS) is:
\[ WSS = \frac{7 - 1}{31 - 1} = \frac{6}{30} = 0.2 \]
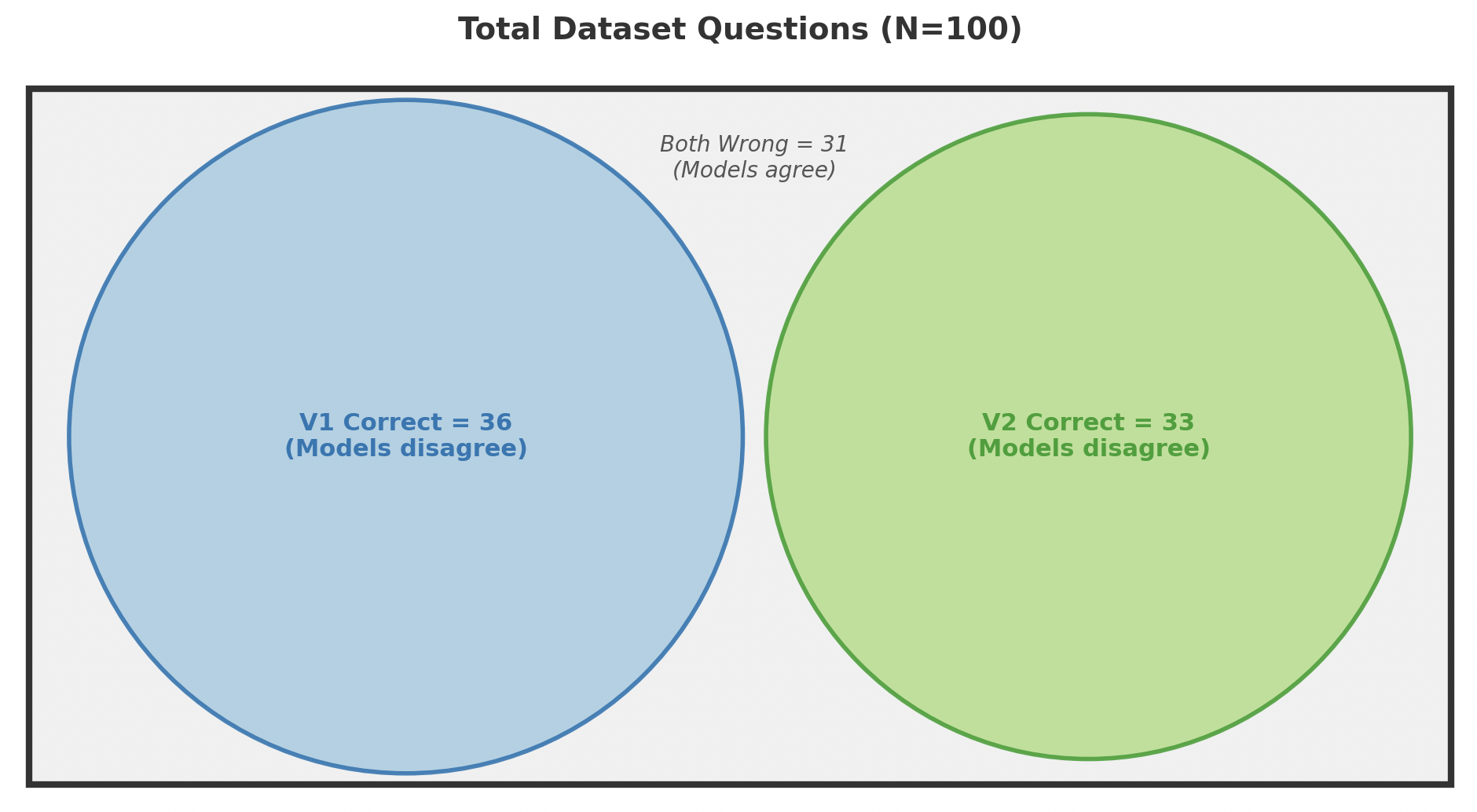
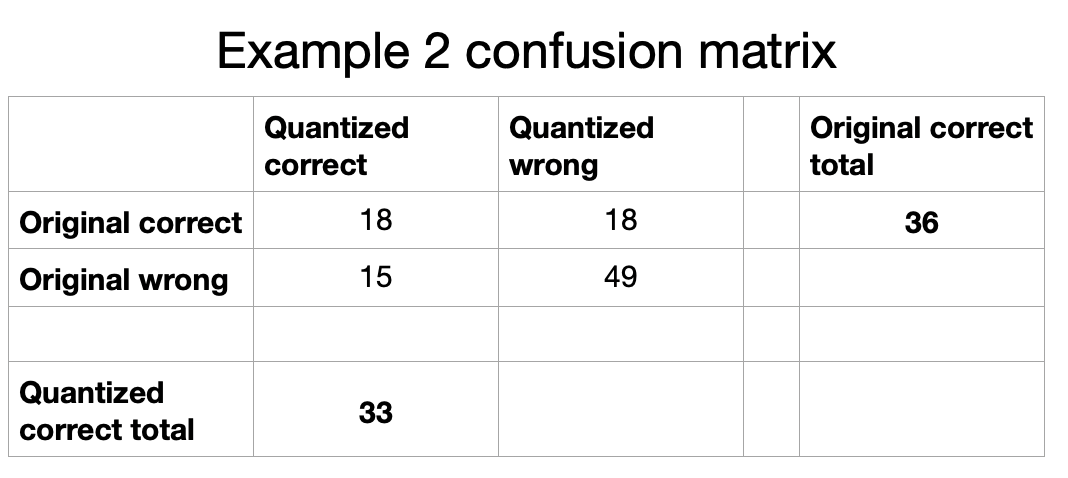
Let's look at a lower accuracy scenario. V1 gets 36 out of 100 right, whereas V2 gets only 33 right. Suppose V2 correctly answers 18 of the 36 questions that V1 got right, but misses the other 18. Additionally, V2 gets 15 questions right that V1 missed. This implies that the two versions disagree on 33 questions out of 100.
For the values of 36 and 33:
The Weidman Swap Score is:
\[ WSS = \frac{33 - 3}{69 - 3} = \frac{30}{66} = 0.455 \]
WSS is most relevant when stability of a new model version relative to a baseline model matters. In the majority of cases when comparing two models or systems, this is not of primary, and possibly not even of secondary, importance: if a new architecture results in a model having 80% accuracy, over the prior version's 75% accuracy, you may not care (WSS could still be informative-a high WSS might indicate the newer model has mastered different aspects of whatever subject the benchmark was measuring than the older model-but it is less likely to "de-risk" the new model in the same way). By contrast, in comparisons where stability does matter, I expect WSS to be an important sanity check: if accuracy drops from 85% to 84%, while there may be nothing to worry about, if WSS is also close to 1, that could indicate that the quantization or distillation has introduced enough instability that the engineer may choose to experiment with other methods before shipping, even if the 1% accuracy drop is considered small on its own.
For a given accuracy decrease of a model relative to a baseline-due to quantization or distillation, for example-a lower WSS is preferable, suggesting that users of the model will experience more stability and need to do less work to modify any workflows that depend on the model behaving as they expect. As people use LLMs for more and more aspects of their personal and professional lives, and as more and more agentic and even non-agentic software systems which have LLMs as an important component, I expect stability between model versions to become increasingly important1 (though I expect absolute performance to remain paramount); thus, researchers and companies that employ them should get in the habit of using this score to check model stability and/or developing their own methods for checking this. We may even see scenarios where organizations decide users would prefer a model with a slightly larger drop in accuracy with a much lower WSS; I leave those judgment calls to the researchers, product managers, engineers, and executives who have to make them.
In the short-to-medium term, I look forward to seeing what reporting of WSS uncovers about how stable or unstable existing quantization and distillation methods are, and I hope it enables the industry to make more informed tradeoffs between absolute performance and consistency between model versions going forward.
Below is Python code that takes in two ordered arrays which are either boolean or 1s and 0s, indicating whether each of two model versions got each question in a dataset correct, and returns the relevant metrics including the Weidman Swap Score:
def swap_metrics(correct_v1, correct_v2):
assert len(correct_v1) == len(correct_v2)
N = len(correct_v1)
M1 = sum(correct_v1)
M2 = sum(correct_v2)
swap_outs = sum(c1 and (not c2) for c1, c2 in zip(correct_v1, correct_v2))
swap_ins = sum((not c1) and c2 for c1, c2 in zip(correct_v1, correct_v2))
dis = swap_outs + swap_ins
min_dis = abs(M2 - M1)
max_dis = min(M1 + M2, 2 * N - M1 - M2) # 2N - M1 - M2 = (N - M1) + (N - M2)
# Handle the (rare) degenerate case where min_dis == max_dis.
if max_dis == min_dis:
wss = 0.0
else:
wss = (dis - min_dis) / (max_dis - min_dis)
return {
"N": N,
"M1": M1,
"M2": M2,
"swap_outs": swap_outs,
"swap_ins": swap_ins,
"disagreement": dis,
"min_dis": min_dis,
"max_dis": max_dis,
"wss": wss,
}1 This conclusion is influenced by my time at SentiLink, where we built fraud models used by banks and lenders. We cared a lot about stability from model version to model version because our customers did. Stability is very important in regulated and/or "infrastructural" industries, of which financial services is both; you wouldn't want to wake up one day and see that your FICO score had changed by a lot because FICO moved to a slightly-more-accurate model that nevertheless resulted in a lot of swaps. I came up with the idea for this specific score after leaving SentiLink and never saw this specific metric computed while I was there (while we cared about model stability, we did not quantize or distill models as is commonly done in more "pure AI" settings). ↩