Attention, Single and Multi-Head

Updated: January 2, 2026

Hand-drawn overview diagram of self-attention and multi-head attention.

Much can and has been written on attention, and for good reason: not only is it probably the single most important operation in modern AI models, it can be hard to grok. The original paper that described the now-ubiquitous "Multi-Head Attention" pattern, Attention Is All You Need (sort of the "Bitcoin whitepaper" of modern AI), is ten technical pages, and originally shipped with an implementation in the powerful but notoriously difficult TensorFlow framework (now buried in this archived GitHub repo) - even when folks published simplified PyTorch implementations, the 4D Tensor reshapings were hard to map to the operations and diagrams from the paper. Several technical writers published deep dives breaking these simplified steps down even further; despite this, in my experience, few people can give a "whiteboard-level" overview of the different components of Attention and how they fit together. Thus, this post adds yet another attention explainer to this universe; the goal is that readers will be able to understand not only the high level structure of Attention, but also where FlashAttention fits in, and straightforward implementations they can dive deeper into if they want.

Quick background on attention

Attention is used to process sequences, specifically sequences where each element is represented as a vector, as is the case with language models where the sequence of vectors represents a sequence of tokens. Like other sequence-modeling building blocks (historically: RNNs, and their evolved variants, LSTMs and GRUs¹), Attention blocks take in a sequence of token vectors and output a sequence of new, “refined” token vectors. So on one level, Attention is yet another composable neural network block, as with its precursors. Indeed, the Attention Is All You Need paper showed that Multi-Head Attention worked well specifically inside a broader “sequence-to-sequence” architecture they called a Transformer. If you want to see what this looks like in straightforward PyTorch code, here is a clean Transformer implementation; the x = self.att(x) line applies multi-head attention.

So what actually happens inside one of these "Attention blocks"?

Inside an attention block

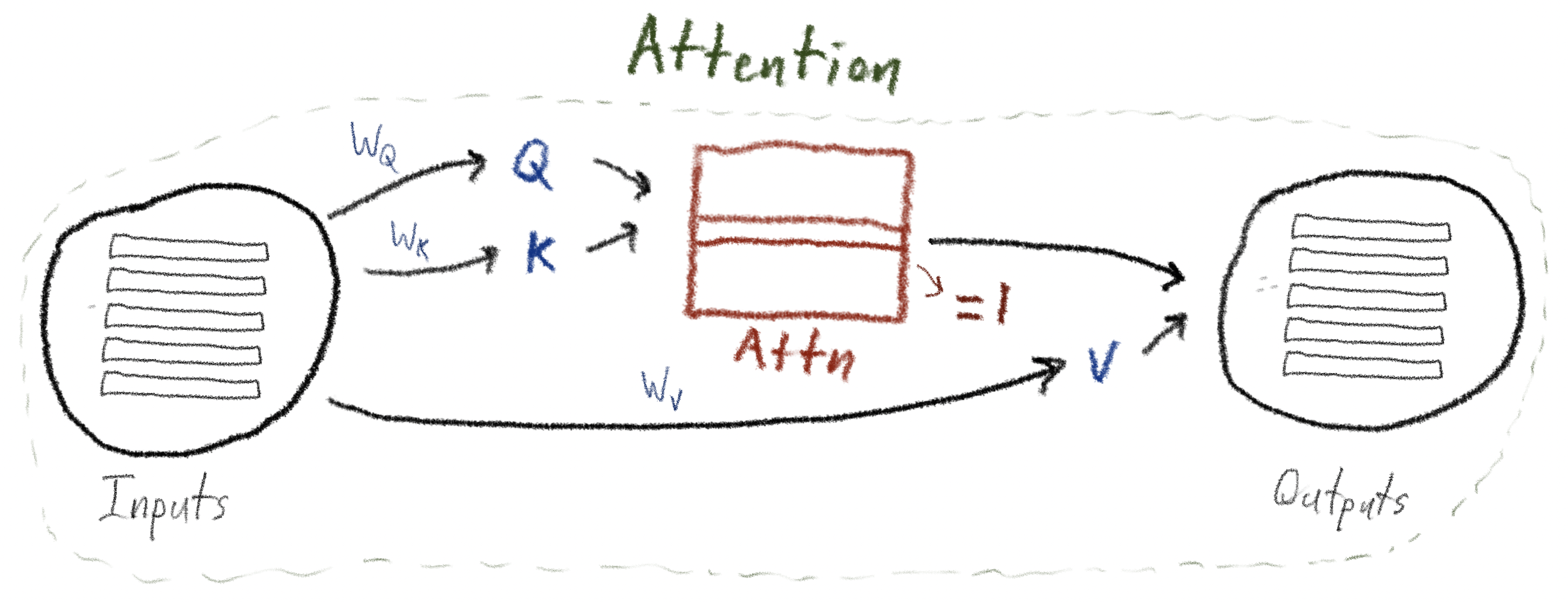
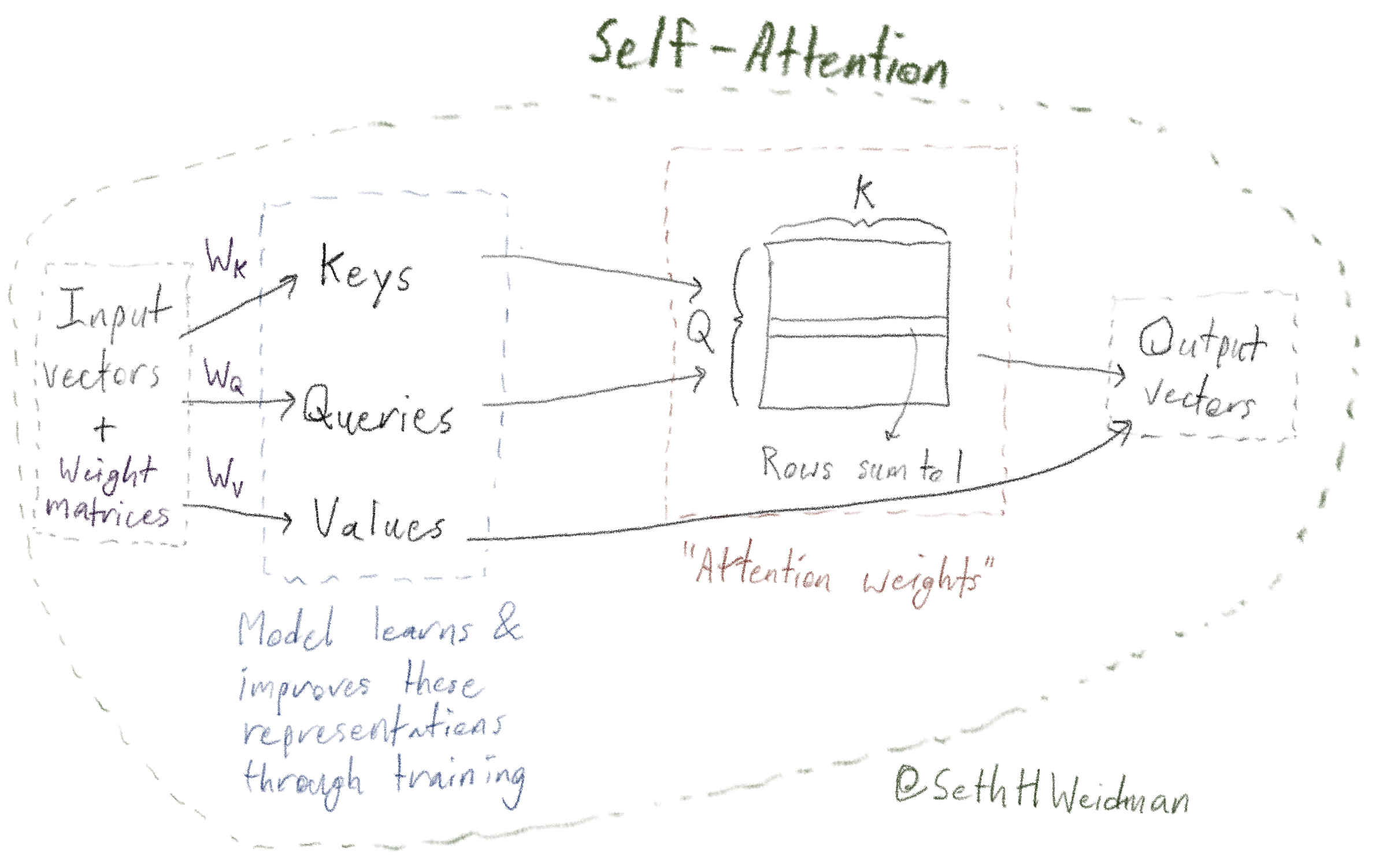
We focus here on Attention blocks that are part of LLMs, with the goal of helping the LLMs generate "good next tokens" given a sequence of prior tokens. We want these blocks to be able to generate an updated representation for each input token, after the block, that can optionally “take into consideration” or, to use the term commonly used in Attention, "attend to" each of the prior tokens². Attention achieves this with an approach loosely motivated by database retrieval: it starts by creating three different representations of each token - queries (Q), keys (K), and values (V) - using three distinct sets of learnable parameters (allowing the representations themselves to be refined as the model is trained). Queries and keys together let the model learn, for each token: “of all the tokens that came before this token, including this one, which tokens should I ‘pay attention to’?” These quantities are known as the attention weights for that token; they sum to 1. The final output vector of each token, at the end of the whole Attention operation, is a weighted average of these learned values V, weighted by the attention weights (which were generated by the queries and keys).

Note: Because the queries, keys, and values are all derived from the same input sequence in the context of LLMs, this variant of Attention is called Self-Attention; this is how we refer to it in the following diagrams.

Below is a diagram that summarizes this; each thick black line from an element indicates that that element is an input to a matrix multiplication. Note that three key weight matrices are used: \(W_Q\), \(W_K\), and \(W_V\), for the queries, keys, and values, respectively. These are each model_dimension by model_dimension; this enables each token vector to have the same model_dimension output length as its input.

Jumping ahead to the implementation, note that in these lines we define three weight matrices in the `__init__` method of the `SingleHeadSelfAttention` class, as you'd expect based on the description above.

Hand-drawn diagram of self-attention: input vectors produce queries/keys/values, which form attention weights that combine values into output vectors.

Multi-head attention

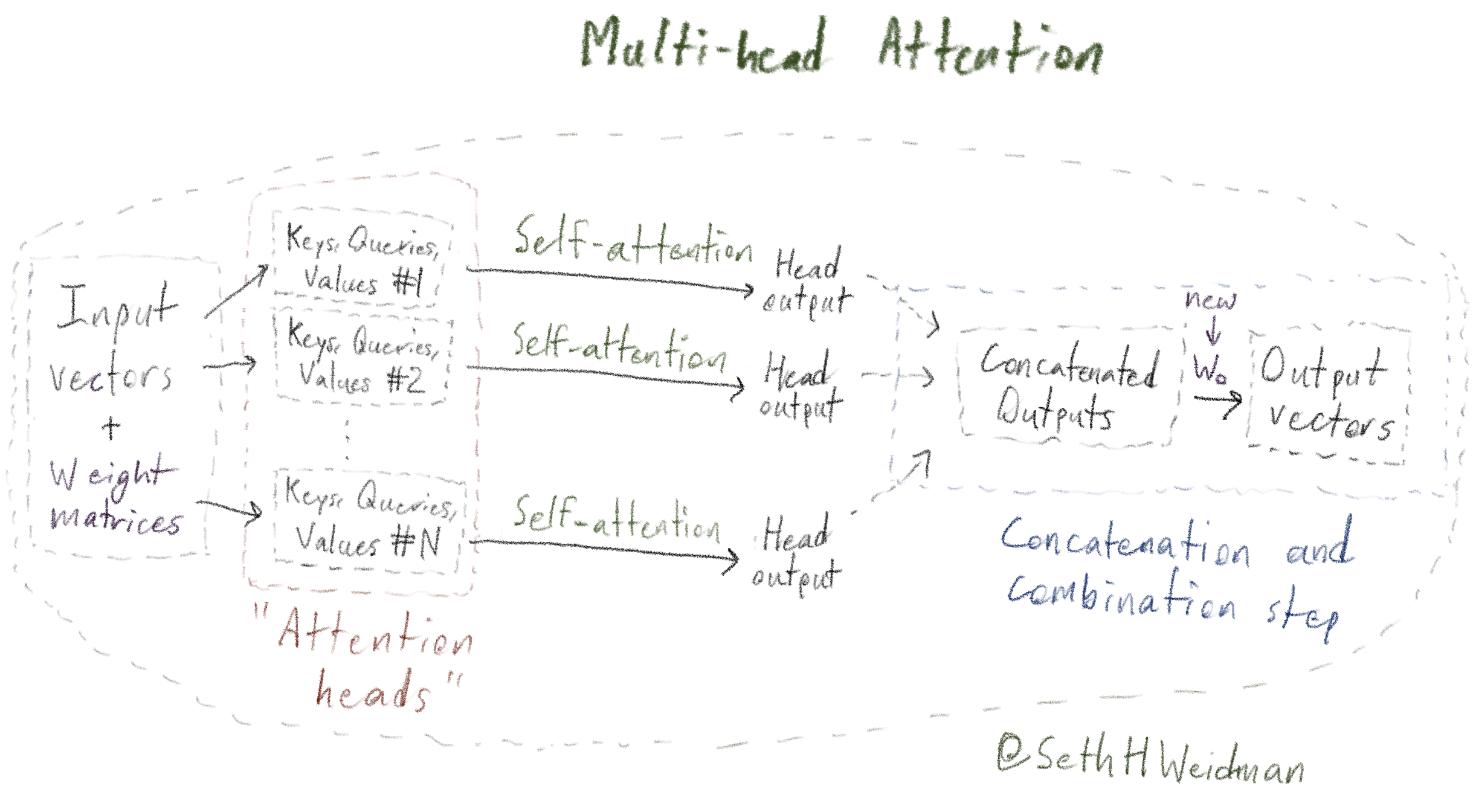
The Attention is All You Need paper didn't just suggest using one big Self-Attention operation; it proposed a variant known as Multi-Head Attention. Mechanically, it works like this:

The \(W_Q\), \(W_K\), and \(W_V\) matrices are "split up along the output dimension" to create \(N\) different "heads". Concretely, this means that if the input vectors originally have length model_dimension, then each head will have dimension model_dimension / N, which we can define as head_dimension. Each of these three matrices \(W_Q\), \(W_K\), and \(W_V\) will thus be model_dimension by head_dimension, and there will be \(N\) of them per type.
We do the attention steps described above on each head independently. Each “head” uses the entire input vector, as well as the three "model_dimension by head_dimension"-sized weight matrices described above to compute its own attention weights and ultimately its own output vectors; that is, it does Self-Attention, but projects the input into a smaller "head" dimension first.
We concatenate these "attention head outputs" back together.
We do one last step to let the model's final representation of each token be a “learned mix” of the concatenated attention head outputs.

The intuition behind trying Multi-Head Attention is that each head could learn independent aspects of the language we are trying to model; one head could focus on grammar in the current sentence, while another could focus on logical consistency with what tokens from long before. It's a bit speculative whether that actually happens within Multi-Head Attention, but empirically, the authors found that Multi-Head Attention did perform better than just doing a one big Single-Head Attention ³ operation. This has been corroborated many times since, and Multi-Head Attention (and variants thereof⁴) is still used within leading LLMs today.

Below is a diagram of Multi-Head Attention in terms of Self-Attention; as before, arrows with solid indicate that the elements are inputs to matrix multiplications, and newly, arrows with dotted lines indicate splitting or concatenating.

Hand-drawn diagram of multi-head attention: token vectors split into heads, each head runs self-attention, outputs are concatenated and mixed into final output vectors.

Implementations

Here are a few implementations with code comments indicating which lines of code correspond to which steps in the diagrams above:

Here is an implementation of Single-Head / Self Attention
Here is an implementation of Multi-Head Attention, naively implemented as several single-head modules whose outputs are concatenated and mixed.
Here is a more standard PyTorch implementation of Multi-Head Attention: it computes each the queries, keys, and values for all heads in just one operation each, reshapes the keys and queries to compute all the attention weights for all heads at once, and finally does another reshaping followed by the mixing of the output vectors across heads.

Attention's Bottleneck and the Motivation for FlashAttention

Much has been written about the computational cost of attention. Here we'll just mention the key advantage, from a computational perspective, of attention over its precursors, as well as its largest downside - a downside which FlashAttention is designed to mitigate.

The bottleneck of the actual computations in attention precursors such as LSTMs was that they had to be processed sequentially: you couldn't compute the representation for token \(t\) until you had computed all prior tokens, 1 to \(t-1\). By contrast, attention computes representations for all tokens at once, allowing parallelism in implementations.
The bottleneck of the computation of Attention is...attention: that is, computing, and especially storing in memory, the "sequence_length by sequence_length" attention matrix itself (the red one in the banner image above). For a 10K token sequence, that's a matrix with 100 million elements, which is 200-400 MB in memory (depending on precision), for a single attention layer; bleeding edge LLMs now advertise 1M token context lengths.

This memory bottleneck is exactly what FlashAttention targets. Working within the memory hierarchy of GPUs, using a very similar tiling strategy to the one described here, as well as the elegant "streaming softmax" trick, it brings the attention computation down from \(O(L^2)\) memory to \(O(L)\) memory. Without tricks like FlashAttention, we might not be able to have LLMs with 100K+ token context windows! These tricks are truly enablers of the AI age in which we're living; they even power the LLMs that helped the author learn this subject and write this blog post that you are now reading, the subject of which is...them! They thus recursively help make the world smarter.

Acknowledgment

An earlier version of this post described one component of the Attention mechanism inaccurately. It has been corrected. Thanks to Chao (Albert) Zhong for pointing it out.

Footnotes

¹ For an overview of RNNs, LSTMs, and GRUs, see Chapter 6 of my book, Deep Learning from Scratch. ↩

² This "prior tokens only" claim is true for decoder-style Transformers used for next-token prediction (LLMs). In encoder-style Transformers such as BERT, where the goal is to create a representation of the entire sequence, tokens can attend to future tokens as well. ↩

³ In comparisons to multi-head attention, self-attention is often referred to as "single-head attention"; this is why in code you'll see that the class name for this operation is SingleHeadAttention ↩

⁴ Sebastian Raschka does a great job covering several of these in the "04", "05", "06", and "07" sections in the bonus content for Chapter 4 of his book. ↩